On Thermal Strains and Residual Stresses in the Linear Theory of Anti-sandwiches

The current study aims to formulate the behaviour of anti-sandwiches that considers residual stresses and thermal strains by means of a layer-wise approach. To this end, the constitutive equations of classical linear elasticity are extended to form the Duhamel-Neumann equations. The direct approach is adopted to project the three-dimensional problem onto two-dimensional surfaces, i.e., each layer of the anti-sandwich is modelled as a single surface that represents the overall behaviour of the layer. The formulation of the problem begins with the decoupling of deformation into independent membrane, bending, twisting and transverse shear modes. The infinitesimal deformation measures are set up on the kinematics of the problem and related to the corresponding kinetic measures via the proposed stiffness relations. The resulting boundary value problem is converted into the equivalent weak form by means of a variational approach. The presented set of equations can be solved inexpensively using various computational approaches such as the finite element method.

Modelling Additively Manufactured Parts Using Direct FE²

This study challenges the Direct FE² to model voids in additively manufactured parts. Some polylactic acid (PLA) tensile coupons—without any voids and with 23% voids—were manufactured using fused deposition modelling (FDM) and tested under monotonic loading. An inhouse Python script was developed to implement the modelling steps of Direct FE² in Abaqus commercial package. A homogenised medium was used in conventional finite element (FE) method whereas discrete modelling of voids was adopted in Direct FE². Despite using the same isotropic elastoplastic material model with progressive damage, the response of Direct FE² was noticeably softer. Although stress concentration around the voids were illustrated in Direct FE², high error values demand further refinements in selecting the representative volume. The applications of this approach can be extended to modelling defects in other complex parts such as auxetic/sandwich structures and composites.

Finite Element Analysis of Natural Fibre Composites Using a Self-Updating Model

The aim of the current work was to illustrate the effect of the fibre area correction factor on the results of modelling natural fibre-reinforced composites. A mesoscopic approach is adopted to represent the stochastic heterogeneity of the composite, i.e., a meso-structural numerical model was prototyped using the finite element method including quasi-unidirectional discrete fibre elements embedded in a matrix. The model was verified by the experimental results from previous work on jute fibres but is extendable to every natural fibre with cross-sectional non-uniformity. A correction factor was suggested to fine-tune both the analytical and numerical models. Moreover, a model updating technique for considering the size-effect of fibres is introduced and its implementation was automated by means of FORTRAN subroutines and Python scripts. It was shown that correcting and updating the fibre strength is critical to obtain accurate macroscopic response of the composite when discrete modelling of fibres is intended. Based on the findings of the current study, considering the effect of flaws on the strength of natural fibres and the fibre area correction factor are crucial to obtain realistic results.

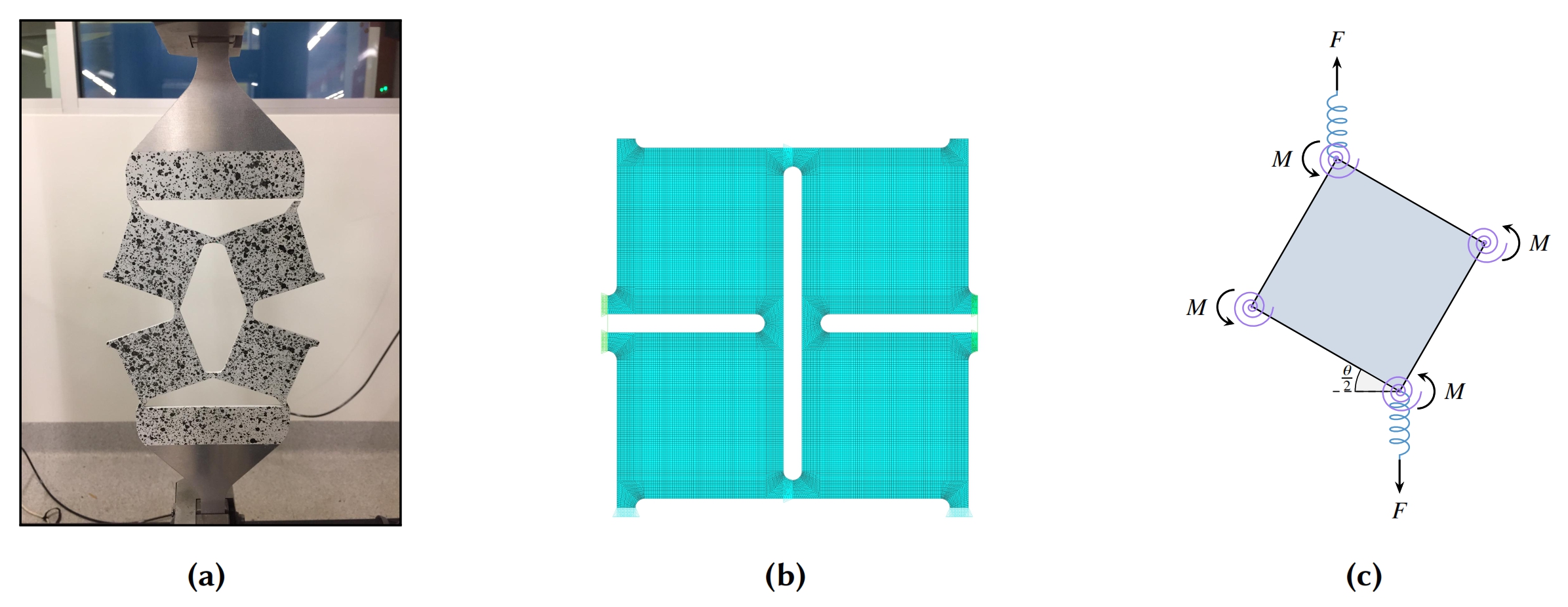
Analyitcal Models for Plastic Behaviour of Rotating Squares

Auxetic structures are emerging as a topic of interest due to their tunable properties for different conditions. Such structures have negative Poisson's ratio as a result of their internal structures and their deformation mechanism at nano or micro levels when uniaxially loaded. Previous studies have demonstrated high energy absorption, increased shear strength, increased plane strain fracture toughness and a high indentation resistance for such structures and materials. These properties make auxetics a prime fit for energy absorbing structures. For this particular arragnement, the rotating squares, it is hypothesised that due to concentration of stresses in the hinges, it is a safe assumption to consider the squares perfectly rigid even in large deformations; however in the hinges, the stretch mechanism starts to dominate as the rotation angle increases. Therefore, it is assumed that rigid square elements rotate about stretchable corner hinges. In this ongoing research, the additional DoF was included into the analytical model and the deformation response was restated consisting of both translational and rotational stiffness of the hinges. Later, the effect of introduced DoF was investigated in finite element models for different hinge stiffnesses. The main idea is to extend the relations to plastic behaviour with an attempt to improve energy dissipation.